UCRL--50400, Vol. 6, Rev. 5
EPDL97:
the Evaluated Photon
Data Library,
'97 Version
by
Dermott E. Cullen
John H. Hubbell *
Lynn Kissel
University of California
Lawrence Livermore National Laboratory
P.O. Box 808
L-59
Livermore, CA 94550
Contact
tele: 510-423-7359
e. mail: cullen1@llnl.gov
* Room C-314 Rad. Phys.
National Institute of Standards and Technology
Gaithersburg, MD 20899
September 19, 1997
Abstract
The Evaluated Photon Data Library, 1997 version (EPDL97), is designed for use in photon transport calculations at Lawrence Livermore National Laboratory. This library includes photon interaction data for all elements with atomic number between Z = 1 (hydrogen) and 100 (fermium), including: photoionization, photoexcitation, coherent and incoherent scattering, and pair and triplet production cross sections. For use in applications data is provided for all elements over the energy range 1 eV to 100 GeV. This report documents the sources and treatment of the data included in this library. EPDL97 completely supersedes the earlier 1989 version of EPDL and it is highly recommended that users only use the most recent version of this library.
Acknowledgments
We thank the many users of the 1989 version of EPDL (referred to below as EPDL89) who have supplied extremely useful feedback to us.
Since the release of EPDL89 in October 1989, the response from users in terms of feedback has been extremely useful in improving the data. We strongly encourage all users of EPDL97 to supply your feedback to us; we can all gain from your experience.Terminology
In this report we will be discussing coherent and incoherent scattering. In general the term coherent scattering means that the amplitudes from contributing component amplitudes (for example, Rayleigh scattering, nuclear Thomson scattering, nuclear resonance scattering, Delbruck scattering) must be added preserving their relative phases (i.e., add coherently) and then squared to define a cross section. In contrast, incoherent scattering amplitudes are first squared and then added together to define a cross section. Note in particular that coherent scattering does not refer to a coherent multiphoton state, such as in a laser; all of the data in EPDL97 refer to single-photon processes.
In general Elastic and Inelastic scattering refer to the physically observable relationship of the energy of the incident and scattered photons. For elastic scattering the incident and scattered photon energy is the same, while in inelastic scattering the incident and scattered photon energies are different. Note, in general all elastic processes are not necessarily coherent and all inelastic processes are not necessarily incoherent.
The above is in general. In the specific case of EPDL97, we will define incoherent scattering, our only inelastic scattering process, as Compton scattering by bound electrons. Similarly we will define coherent scattering, our only elastic scattering processing, as Rayleigh scattering from the bound electrons. These are the only scattering processes included in EPDL97. Therefore in the specific case of EPDL97 the terms coherent, elastic and incoherent, inelastic can be used interchangeably. However, the reader should be aware, based on the preceding paragraphs, in general these terms are not physically equivalent.
EPDL97 vs. EPDL89 Contents
Compared to EPDL89 [1, 2, 3, 4], EPDL97 has been updated to include all of the most recently available theoretical and experimental data. In this process EPDL97 has taken advantage of the tremendous increase in computer power and storage capacity since EPDL89 was released. Data has been calculated to higher precision and includes more data points to allow more accurate interpolation between tabulated data points.
To briefly summarize the similarities and differences between EPDL97 and EPDL89,
Similarities
1) Both include data for elements Z = 1 (hydrogen) through 100 (fermium).
2) Both include cross sections for photoionization, coherent and incoherent scattering, pair and triplet production, form factors, scattering functions, anomalous scattering functions, and average energy all secondary particles, including the initial scattered photon, as well as any secondary photons, electron and positrons. For photoionization both include cross sections for all subshells.
3) Both include data up to 100 GeV.
4) Both use the same atomic parameters, in particular for consistency with the Livermore Evaluated Electron Data Library (EEDL) [5], both use the same photoionization subshell binding energies.
Differences
5) EPDL97 includes data down to 1 eV, whereas EPDL97 includes data down to 10 eV. The extension to lower energy was primarily to allow a complete description of photoionization, that is required to accurately calculate anomalous scattering factors.
6) EPDL97 includes photoexcitation data, that was not available at the time that EPDL89 was released.
7) EPDL97 includes improved anomalous scattering factors and coherent scattering cross sections, based on the photoionization and now available photoexcitation cross sections.
8) EPDL97 is based on more recently available theoretical and experimental data.
For a more detailed description of the differences between EPDL89 and EPDL97 contact D. E. Cullen for a copy of a much longer report including plots comparing all of the data from the two libraries. This is a very large and limited edition report, so please only request a copy if you really need to know the details of differences.
EPDL97 vs. EPDL89 Documentation
All earlier versions of the documentation for EPDL [2] were large books containing graphical and tabulated data. It is no longer practical for us to produce books in this form, for several reasons: 1) it is very expensive to publish large books, 2) the data in books is quickly out-of-date, 3) books do not provide users with the actual data in the form they need for use on their computers.
As a substitute for these books we now offer the interactive graphics code EPICSHOW [6] that is designed to run on virtually any computer. EPICSHOW includes data for: photons, electrons, neutrons, and light charged particles. Compared to books this code offers the following advantages: 1) it is inexpensive to maintain and distribute, 2) its data can be easily maintained up-to-date, 3) users now have the data available on their computer (with a book you could only look at it), 4) you can examine the data graphically on your computer screen in any detail that you want, 5) you can obtain simple tabulated output, that can be easily re-formatted for use in your applications, 6) you can obtain color and/or black/white Postscript output for use in your lectures or reports.
EPICSHOW has now been available for several years, and based on feedback from users, this code is much preferred by users over the earlier books, which did not make the actual data available to users.
This report was written in Microsoft Word format. In order to allow distribution of this report on-line, it has been constrained to be as compatible as possible for use with a variety of word processors. In particular equations and figures (whose format varies between word processors) have been avoided. The figures that are distributed with the published report, are included with the on-line report as Postscript formatted files that can be viewed with programs such as Ghostview, that are freely available on the Web.
Whats Missing: Data Needs
This library only includes data for atomic processes: photoionization, photoexcitation, coherent and incoherent scattering, and pair and triplet production. This data is only applicable to cold, neutral, isolated atoms.
Users should be aware that for a complete description of photon transport and all secondary particles emitted due to photon interactions their application may require additional data that is not included in this library.
This library does not include data for all photon-atom interactions, and some details of the interactions are not included in the library. While these interaction details are not expected to be generally important in bulk radiation transport in cold material, they can nevertheless be very important over limited photon energy ranges, or in situations such as in diagnostic measurements. For example, we only consider single-photon interactions with isolated, ground-state atoms, neglecting interactions with ions and excited states. We do not consider atoms in environments (e.g., solid-state effects, plasmas, external electric or magnetic fields) which can have significant effect on the cross sections near the photoeffect thresholds of inner-shell electrons, and completely alter the cross sections near the thresholds of outer-shells.
We have not included details of photon polarization, assuming an unpolarized source of photons and summing over polarization of all outgoing photons. However, photon-polarization can be important in some cases. For example, right-angle elastic (coherent) scattering will result in a highly polarized beam, even if the incident photon beam is unpolarized. A recent treatment of polarization effects on multiple scattering in photon transport is given in reference [7].
We have not included resonance effects in inelastic (incoherent) scattering, as this is currently beyond our calculational capabilities (see, the section on S-Matrix Theory). However, just as we observe enhancements in the elastic (coherent) scattering cross section included in this library, we expect similar enhancements in inelastic (incoherent) scattering. Raman scattering (inelastic photon scattering resulting in excitation of atoms) [8] is a particular component of the resonance effects in inelastic scattering that have been neglected. Delbruck and nuclear scattering are also not included in EPDL97; these become important above about 1 MeV.
Multiphoton processes have been neglected. The simplest examples include two-photon excitation, absorption and scattering. Generally multiphoton processes are a small fraction (generally 1 % or less) of the single-photon process.
This library includes form factors and scattering functions that can be used to define scattering angle and energy distributions. However, it does not include differential cross sections.
EPDL97 also does not include any photonuclear data. Photonuclear interactions can contribute as much as 5 - 10 % to the total photon interaction cross section in a fairly narrow energy region usually occurring somewhere between 5 and 40 MeV, depending on the location of the giant resonance of the target nucleus. As yet a systematic compilation of photonuclear data is not available for the entire range of elements included in EPDL97 (Z = 1 through 100).
We would be very interested to collaborate with anyone who may be able to provide additional data for inclusion in this library.
S-Matrix Theory
Initially we had hoped to include data based on the most recent developments in S-Matrix theory, for both coherent and incoherent scattering. However, as yet inclusion of data based on S-Matrix theory for a general purpose library, such as EPDL97, is still be beyond our calculational capabilities. For a recent status report on S-Matrix theory of incoherent scattering, see reference [9].
Although S-Matrix data is not yet available for all elements and energy ranges included in EPDL97, we should mention that it is available for specific elements and energy ranges, (see, the section of Other Available Data).
Other Available Data
As mentioned above, EPDL97 is designed to meet the needs of users at Lawrence Livermore National Laboratory for use in photon transport calculations. For a general purpose library, such as EPDL97, covering the entire periodic table, and a wide energy range, it was necessary to interpret all of the available photon data in an attempt to best meet our needs.
We should point out that EPDL97 is only one possible interpretation of the available photon data. For your individual applications you may find that other available data better meets your specific applications. Below we mention a few additional resources that you may find of use.
NIST
The National Institute of Standards and Technology (NIST) maintains a large number of databases; several of these deal directly with photon-atom interactions. A catalog of NIST standard reference data products is available via the World Wide Web (WWW) at,
http://www.nist.gov/srd/
Most closely related to the information contained in EPDL97 are,
NIST Form Factors, Attenuation & Scattering Tables (FFAST) - primary interactions of x-rays with isolated atoms (Z=1-92) for energies from 1 eV through 1 MeV.
NIST X-Ray and Gamma-Ray Attenuation Coefficients and Cross Section Database - provides cross sections and attenuation coefficients for elements Z=1-100 for energies from 1 keV through 100 GeV.
NIST Data for Atomic Spectroscopy (DAS) - contains wavelengths, transition probabilities and energy levels for many ionization stages of elements Z=1-28.
NIST Spectroscopic Properties of Atoms and Atomic Ions Database - provides access to emission wavelengths for all neutral atoms and their first four ionization stages.
Henke
For photon energies 50 eV through 30 keV and atoms Z=1-92, Henke, et al. [10], provide tables of photoabsorption, scattering, transmission and reflection data. These data are a synthesis of a large body of experimental measurements and theoretical calculations. Additionally, a tutorial section of their 1993 publication gives prescriptions for the performance of x-ray optical elements, such as filters, scatterers and synthetic multilayers. Eric Gullikson maintains the WWW site at Lawrence Berkeley National Laboratory wherein this data is available on-line,
http://www-cxro.lbl.gov/optical-constants/
Kissel
For those interested in elastic scattering per se, Kissel and co-workers have exploited the S-Matrix method to compute ab initio elastic scattering amplitudes that avoid many of the approximations contained in simpler approaches (see, for example, Kissel and Pratt, 1985 [11]). A significant feature of the S-Matrix approach is complete photon-polarization information and accurate predictions of the scattering angular distributions.
More recently, results of the S-Matrix method have been used to do a careful investigation of the validity of form factor and anomalous scattering factor approaches to scattering (Kissel, et al., [12]). The results of this approach have been used to define the improved EPDL97 elastic (coherent) scattering data.
Kissel maintains the Elastic Photon-Atom Scattering WWW site at Lawrence Livermore National Laboratory,
http://www-phys.llnl.gov/V_Div/scattering/elastic.html
At this site one can access S-Matrix, anomalous scattering factors, and form factor predictions for all neutral atoms Z=1-99 and photon energies 0-10 MeV.
The S-Matrix approach has also been applied to inelastic scattering by Suric, Bergstrom and co-workers (Suric, et al., [13]). Their initial survey of widely used simpler approximations to inelastic scattering from inner shell electrons(Bergstrom, et al., [14]) pointed out significant deficiencies in many situations. Unfortunately, this research has not matured to the level that systematic tabulations of improved inelastic scattering predictions can yet be prepared. See also, [9].
Related Livermore Data Bases
EPDL97 is one of a set of data bases developed at Lawrence Livermore National Laboratory to allow consistent coupled photon-electron transport calculations. Use of the combination of these data bases is consistent in the sense that both photons and electrons use exactly the same atomic parameters, such as photoionization subshell binding energies.
The data bases include,
EPDL97 - The Evaluated Photon Data Library, includes data to describe the transport of photons, as well as the initial generation of secondary particles, such as the primary electron emitted due to photoionization or Compton (incoherent) scattering, as well as the electron/positron pair emitted due to pair production.
EEDL - The Evaluated Electron Data Library [5], includes data to describe the transport of electrons, as well as the initial generation of secondary particles, such as the primary photon due to bremmstrahlung, as well as the primary electron due to inelastic scattering and electroionization.
EADL - The Evaluated Atomic Data Library [15, 16], includes data to describe the relaxation of ionized atoms back to neutrality, during which photons (fluorescence x-rays) and electrons (Auger and Coster-Kronig) are emitted. It is assumed that the relaxation of an ionized atom is independent of how the atom was ionized, so that this data may be used to describe the relaxation of atoms that were ionized due to either photoionization or electroionization.
EXDL - The Evaluated Excitation Data Library, includes data to describe photoexcitation lines. EXDL is distributed with EPDL97, but maintained as a separate file of data, in order to simplify its use in applications.
One of the constraints on EPDL97 is that it remain consistent with the existing data bases. In particular, EPDL97 has been constrained to use exactly the same atomic parameters as the other data bases; this point will be discussed in more detail below.
Sources and Treatment of Data
Atomic Parameters
All of the data included in EPDL97 draws on currently available photon data, and is based heavily on an interpretation of the Other Available Data sources, described above. All of the data in EPDL97 is for cold, neutral, isolated atoms of each element. No data is provided for combinations of elements, e.g., H2, H2O, etc.
For consistency with the Livermore Evaluated Electron Data Library (EEDL) [5], EPDL97 uses the same photoionization subshell binding energies as were used in EPDL89 and EEDL. These are based on the data of Scofield [17]. For a complete list of atomic subshell binding energies see [2]. Comparison with more recent values shows differences of less than 1 %, which is small compared to the differences we expect due to elements combining into radicals or compounds, e.g., the K shell binding energy of H is 13.6 eV, and that of 31 is 16.4 eV, about 21 % higher. For use in our applications we judge consistence between our photon and electron data to be more important than the "exact" values of elemental binding energies. This will effect accuracy only over narrow energy ranges near photoionization edges.
For use in your applications you may prefer to make a different decision concerning atomic parameters; see above, the section on Other Available Data.
Photoionization
The sources of photoionization data include data calculated by Kissel using Scofields subshell cross sections [18] from the edge energy up to 1 MeV and Hubbell's [18, 19, 20] total photoionization cross sections from 1 keV to 100 GeV. These two sets of data have been combined to define subshell cross sections from the edge energy to 100 GeV. From the edge to 1 MeV, the subshell cross sections and total, defined as the sum of the subshells, are based on Scofields data. From 1 MeV to 100 GeV the total is based on Hubbells data [21]. At 1 MeV the total photoionization is identical from both sources, so that joining the two sets could be done in a consistent manner. Scofields subshell cross sections have been extended from 1 MeV to 100 GeV by insuring that the sum of the subshell cross sections is equal to Hubbells total, and maintaining the same ratio between subshell cross sections over the entire energy range from 1 MeV to 100 GeV.
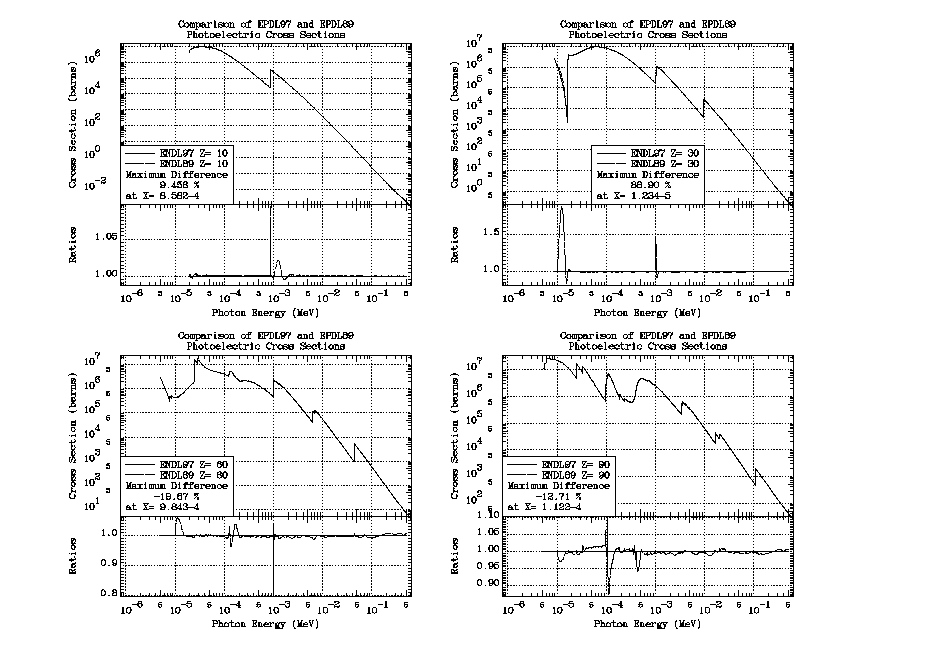
Photoionization cross sections are included for all subshells from the energy of its ionization edge up to 100 GeV. The total photoionization cross section (the sum of the subshell cross sections) is also included. See the appendix for a comparison of EPDL97 and EPDL89 photoionization cross sections. In the appendix you will see that the cross sections are in good agreement, except near edges, and in some cases where more recent calculations and measurements have improved the EPDL97 data; particularly low energy data for outer subshells. The smaller differences (fraction of 1 %) at higher energies are due to more densely tabulated energy points that have improved the EPDL97 data.
Photoexcitation
Photoexcitation data are those of Kissel, who directly computed the relativistic multipole bound-bound oscillator strengths (see, for example, Scofield, 1975 [17]) between all occupied and empty orbitals of each atom. Direct numerical calculations were performed for principle quantum numbers up to n = 20, with extrapolation to higher values as needed, to assure that all oscillator strengths through 10-6 of the maximum value were evaluated.
Unlike the other cross sections, which are tabulated and continuous in energy, the excitation data is defined by tabulated discrete energies and line strengths. The line strengths are in barns per atom.
It should be noted that this excitation data is an approximation to well known infinite series of excitation lines. It is approximate in the sense that obviously a tabulation of finite length is not exactly the same as an infinite series of lines. However, the photoexcitation data included in EPDL97 reproduces the important integral (over energy) effects that we are interested in, particularly the important integral in energy used to define anomalous scattering factors.
Coherent Scattering
Form Factors
The form factors are those of Hubbell [22, 23, 24]. Hubbell has calculated nonrelativistic, relativistic, and modified relativistic form factors. Based on Hubbells recommendation the data included in EPDL97 are his nonrelativistic form factors, which are currently the most widely used of Hubbells form factors. These are the same form factors used in the earlier EPDL89 library.
In theory the most consistent treatment of coherent scattering would have been to use relativistic form factors with our anomalous scattering factors to define the coherent scattering cross section; if you wish to use this approach the data you need is available at Kissels web site (see, Other Available Data, above). In practice extensive photon transport calculations have verified Hubbells recommendation, that for use in photon transport applications it is better to use his nonrelativistic form factors.
Anomalous Scattering Factors
Anomalous scattering factors are those of Cullen [25] computed using the relativistic dispersion relation as detailed in Pratt, et al. (1994) [26] in conjunction with the EPDL97 photoionization and photoexcitation data. Since the relativistic photoelectric cross section varies as 1/E at high energies, the relativistic dispersion integral is not convergent without considering other contributing effects. As Pratt, et al. [26] note, contributions from bound-electron pair production contribute to the same order and must be included for convergence of the integral. We estimate this contribution to the dispersion integral using analytic semi-relativistic expressions due to Costescu, et al. (1994) [27]. For more details on our utilization of bound-electron pair production (wherein the electron of the pair is created in a bound state of the atom) in evaluation of the relativistic dispersion relation, see Kissel, et al. (1995) [12].
The resulting anomalous scattering factors vary from a value of -Z at zero photon energy to a non-zero high energy limit as defined by Kissel and Pratt (1990) [28]. The accuracy of the convergence of our numerical anomalous scattering factor to -Z at low energy provides us with an important check on our numerical procedures as this limit is a statement of the relativistic Thomas-Reiche-Kuhn sum rule (see, Kissel, et al. 1995, for more details [12]). Note, using the convention defined here, the high energy limit is equal to the values defined by Kissel and Pratt, and is negative.
Anomalous scattering factors are included from 1 eV to 10 MeV. At higher energies they become progressively smaller and approach the limit of Kissel and Pratt [28], and have progressively less effect on the coherent cross section. By 10 MeV they have essentially no effect on the coherent cross sections and are not considered above 10 MeV.
Coherent Cross Sections
The coherent cross sections are those of Cullen based on the combination of Thomson scattering, form factors, and anomalous scattering factors, which were numerically integrated to define the cross sections.
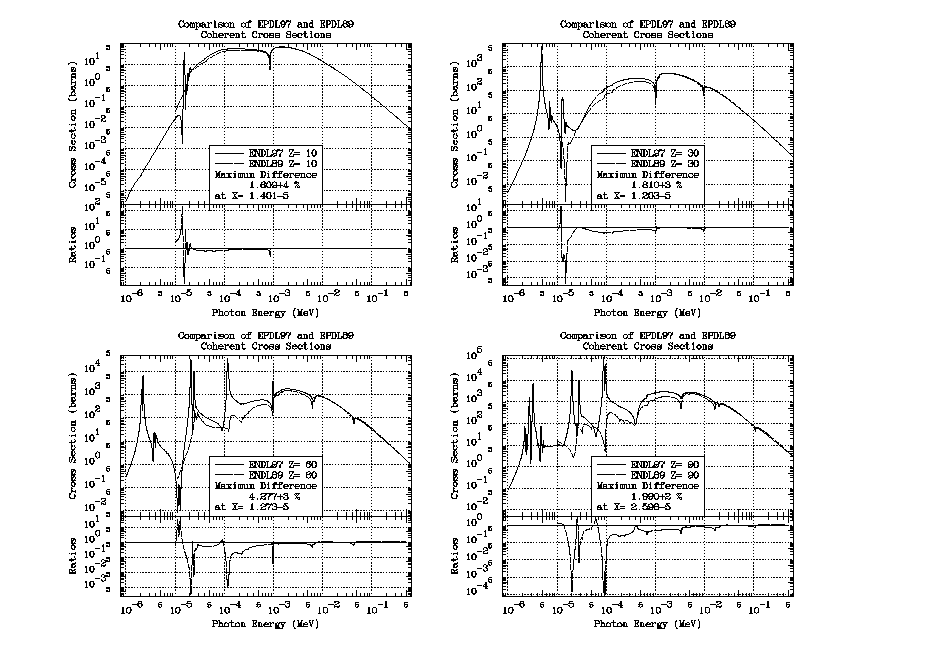
Coherent scattering cross sections are included from 1 eV up to 100 GeV. See the appendix for a comparison of EPDL97 and EPDL89 coherent cross sections. In the appendix you will see differences, particularly at low energies due to the now available photoexcitation data that was used to calculate the EPDL97 anomalous scattering factors.
Incoherent Scattering
Scattering Function
The scattering functions are those of Hubbell [22, 23, 24]. For use in EPDL89 Hubbells scattering functions were extended from 100 eV down to 10 eV. For use in EPDL97 they were further extended down to 1 eV, and the method of extension below 100 eV was improved to obtain the correct Z dependent variation.
Incoherent Scattering Cross Sections
The incoherent cross sections are those of Cullen based on the combination of Compton scattering described by the Klein-Nishina formula and scattering functions that were numerically integrated to define the cross sections.
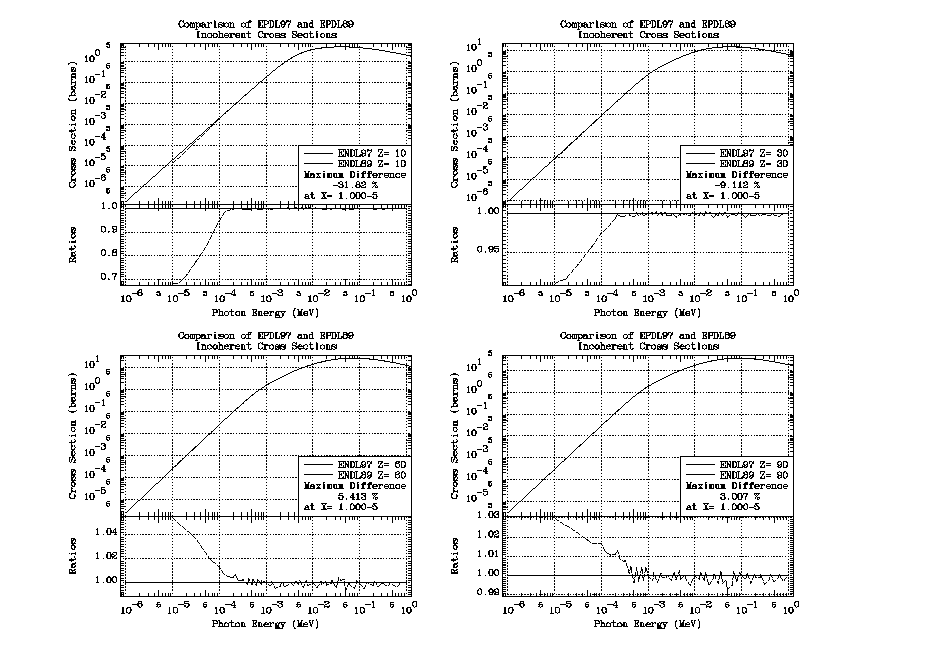
Incoherent scattering cross sections are included from 1 eV up to 100 GeV. See the appendix for a comparison of EPDL97 and EPDL89 incoherent cross sections. In the appendix you will see differences, particularly at low energies due to improved extension of the scattering functions below 100 eV. The smaller differences (fraction of 1 %) at higher energies are due to more densely tabulated energy points that have improved the EPDL97 data.
Pair and Triplet Production
The pair and triplet production cross sections are those of Hubbell [21]. These are the same data used in the earlier EPDL89 library.
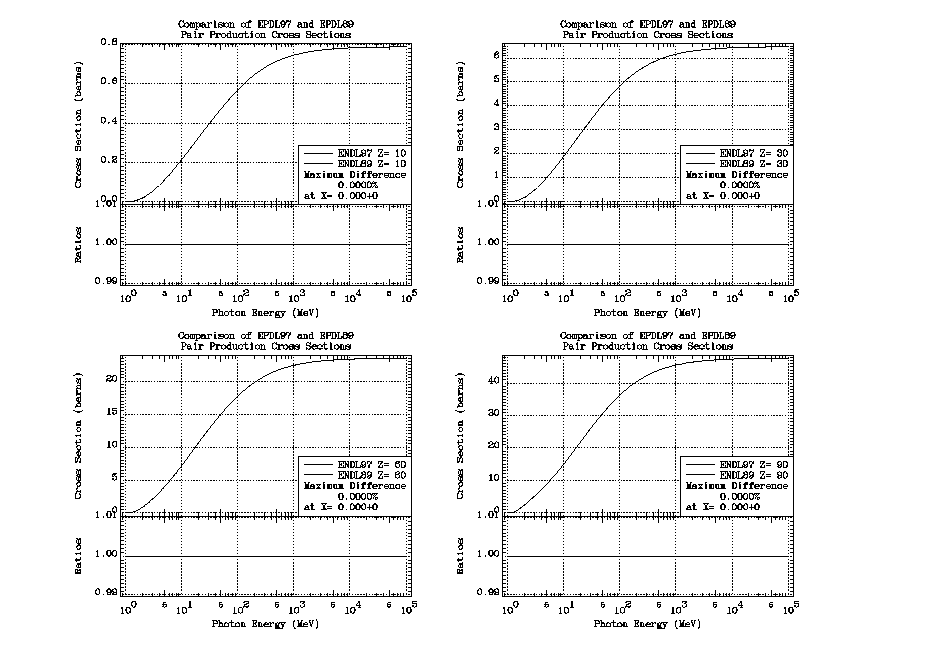
Pair production cross sections are included from their threshold at 1.022 MeV (two times the electron rest mass energy) up to 100 GeV. Similarly, triplet production cross sections are included from their threshold as 2.044 MeV (four times the electron rest mass energy) up to 100 GeV. See the appendix for a comparison of EPDL97 and EPDL89 pair production cross sections. In the appendix you will see that the EPDL97 and EPDL89 pair production cross sections are exactly the same.
Average Energy of All Secondaries
In addition to the data discussed above, this library also contains the average energy of all secondary particles, including the initial scattered photon, as well as any secondary photons, electron and positrons. In all cases the objective is to define average secondary particle energies to conserve the total available energy, so that this data can be used to accurately calculate expected values in transport calculations, see [29, 30]. Below we describe how this data is defined.
Photoionization
The incident energy of the photon is divided between all photons and electrons emitted following the ionization event, this includes: the primary electron emitted when the atom is ionized, as well as all photons (fluorescence) and electrons (Auger and Coster-Kronig) emitted as the atom relaxes back to neutrality. The sum of the average energy of all secondary "particles" (x-rays and electrons) is exactly equal to the energy of the incident photon.
Fluorescence (x-ray), Auger and Coster-Kronig (electron) yields as an ionized atomic relaxes back to neutrality are based on the Livermore Evaluation Atomic Data Library (EADL) [15], and the average division of energy between x-rays and electrons has been calculated using the EADL data and program RELAX [16]. A review and tabulation of x-ray fluorescence yields is also given in reference [31].
Photoexcitation
As yet we still do not have data to completely describe the relaxation of excited atoms back to their ground state. It is assumed that an atom is excited, absorbing the photon. No description of how the atom de-excites and returns to its ground state is provided. No average energy of secondaries is provided. The details of what happens following excitation are highly application dependent, and as such how this is treated is left up to the individual users.
Coherent Scattering
The incident energy of the photon is conserved during a coherent scatter. As such the average energy of the scattered photon is equal to the incident energy.
Incoherent Scattering
The incident energy of the photon is divided between the scattered photon and electron. The average scattered photon energy is defined by numerically integrating the product of Compton scattering described by the Klein-Nishina formula and the scattering function (which is designed to compensate for binding effects). The average electron energy is defined as the difference between the incident and scattered photon energies. In this procedure electron binding is not explicitly included, nor is the ionization of the atom and its relaxation back to its neutral, ground state.
Pair and Triplet Production
In pair production the incident energy minus 1.022 MeV is defined to on average be divided equally between the electron, positron pair. The additional 1.022 MeV is the energy required to produce the pair.
In triplet production the additional low energy electron is ignored and the division of average energy is identical to the treatment used for pair production.
Accuracy of Data
In this section we discuss the accuracy of the data that is included in EPDL97. For a more complete picture of the accuracy that you can expect when using this data in applications you should also consider data that is not included in EPDL97; see also, the above section on Whats Missing: Data Needs.
The below table presents a rough estimate of the maximum per-cent (%) uncertainty of the photoionization cross section in various energy ranges. As can be seen from this table, there is still a large uncertainty in the photoionization cross sections at low energy, where photoionization is the dominant process. Therefore although the EPDL97 data has been extended down to 1 eV in order to meet our needs for a complete description for photoionization needed to accurately calculate anomalous scattering factors, users should be aware that there will be a large uncertainty associated with results obtained using the currently available low energy data, i.e., caveat emptor.
Energy Range Solid (%) Gas (%)
1-10 eV...................?....................?
10-100 eV................1000...............20
100-500 eV..............100-200...........10-20
0.5-1.0 keV..............10-20..............5
1.0-5.0 keV..............5....................5
5-100 keV................2....................2
0.1-10 MeV..............1-2.................1-2
0.01-100 GeV...........2-5.................2-5
By comparing subshell parameters from a number of different sources, it can be seen that there is still a disagreement of about 1 % in elemental photoionization edge energies. As discussed above, this is small compared to the variation in edge energies between elements, radicals, and compounds. As stated above, for use in our coupled photon-electron transport calculations, using the "exact" binding energy is not as important as insuring that the same binding energies are used for both photon and electron data. Therefore Scofields subshell parameters [18] are consistently used for both photon and electron data.
The photoexcitation data included in EPDL97 has only been used in combination with the photoionization data to define anomalous scattering factors. Based on the optical theorem [12] we expect the combination of the ionization and excitation data integrated over energy to be equal to Z across the entire periodic table, which it is for the EPDL97 data. Therefore the integral (over energy) strength of the excitation data appears to be quite good. As pointed out above, the EPDL97 representation of the excitation data as a table approximating infinite series, implies that there will be an uncertainty in the energy, strength and obviously the number of excitation lines. However, the photoexcitation data included in EPDL97 includes all of the important detail required for photon transport calculations.
The recently available photoexcitation data used in combination with the photoionization data gives us a complete picture that has allowed us to calculate more accurate anomalous scattering factors. These in turn have allowed us to improve the accuracy of our coherent scattering cross sections. Including anomalous scattering causes very large decreases in the coherent cross section near photoionization edges and a coherent cross section that approaches zero at low energy, as opposed to the constant value obtained using only form factors. Comparisons indicate that use of our anomalous scattering factors yield coherent cross sections that are in close agreement with the results obtained using the more exact S-Matrix theory. However, it should be noted that although the cross sections are in close agreement, there can be large differences between the angular distributions based on S-Matrix theory and those based on form factors and anomalous scattering factors; this is particularly true for large angle scattering where the form factor becomes extremely small. Hubbell estimates that for large angle scattering the results based on form factors can have an uncertainty of a factor of 2, but be aware that large angle coherent scattering is a very low probability event that usually will not have a large overall effect on photon transport calculations.
The incoherent cross section derived by integrating the product of Compton scattering defined by the Klein-Nishina formula and scattering functions, will be accurate at higher energies, but the uncertainty will increase near and below photoionization edges. For consistency all cross sections in EPDL97 have been extended down to 1 eV. At such low energies the uncertainty in the incoherent cross section will be enormous! Fortunately at lower energies the incoherent cross section is unimportant, since the cross section is small compared to the coherent scattering cross section, and incoherent scattering does not result in any significant energy loss by photons. Therefore the enormous uncertainty in the incoherent cross section at low energy should have no practical effect on photon transport calculations.
Based on the Dirac-Hartree-Slater calculations of Chen [32] the Auger (nonradiative) widths for an inner shell vacancy are known to better than 15 % if the inner shells do not decay by Coster-Kronig or super-Coster-Kronig transitions; for these transitions, the widths can be too large by up to a factor of 2. These uncertainties directly effect the competition between radiative and nonradiative yields, e.g., the fluorescence yield.
As yet EPDL97 does not include several types of data, including photonuclear, and Delbruck and nuclear scattering. Photonuclear can have an important effect at higher energies. Delbruck and nuclear scattering become important above about 1 MeV. The status of all these types of data is currently under review, and it is planned that these types of data will be included in EPDL in the future.
Use of the EPDL97 Data
Examples illustrating the appropriate use of EPDL89 are available in a variety of references, see [29, 30, 33, 34, 35, 36]. Here we to try to provide additional guidelines for the use of EPDL97.
In this report we have tried to stress that the ONLY reason EPDL97 has been extended down to 1 eV is to allow us to have a complete description of photoionization data down to the energy of the lowest energy edge. This data is needed in order to consistently define anomalous scattering factors, which is defined in terms of integrals over energy of the photoionization and excitation data. For consistency throughout EPDL97 all cross sections have been tabulated down to 1 eV, below the lowest energy photoionization edge.
However, users should be WARNED that it is NOT intended that photon transport calculations be extended down to such low energies using the EPDL97 data. As can be seen from the above table the uncertainty in the data rapidly increases with decreasing energy. Even more important, from the above discussions of Whats Missing: Data Needs, users should be aware that at very low energies accurate photon transport requires additional data, that is not included in EPDL97.
Here are some broad guidelines are using the EPDL97 data,
1) You can safely and accurately use this data down to about 1 keV.
2) Between 100 eV and 1 keV you can still safely use this data, but your results will be limited by the uncertainty in the data.
3) Between 10 and 100 eV it is neither safe nor accurate to use this data. It is not safe because in performing photon transport calculations once you get below the lowest energy photoionization edge you can end up in a completely unphysical situation where photons are "trapped" (there is no way to absorb them and no mechanism to allow them to lose energy, so they can scatter around forever). Transporting photons in this energy range definitely requires additional data, not included in EPDL97.
4) Between 1 and 10 eV, as far as transport calculations using the EPDL97 data, dont even think about it!!!
With that said, the reader may ask: why do we include any data to such low energies? Our experience has been that this can be described in terms of two themes,
1) Star Trek "Boldly going where no one has gone before" = if there are applications that extend to regions where our data is poorly known (in this case, low energies) our philosophy has always been that it is better to have some data to work with than nothing at all. In this case it is extremely important that if users do decide to use our low energy data in their applications, that they recognize the limitations of the data they are using and the accuracy (or lack there of) in any calculated results.
2) Field of Dreams "Build it and they will come" = our experience has been that pointing out deficiencies in our data, has led to important feedback from users and data experts that has led to significant improvement in our data. In this case we are providing our best estimate of the low energy data, so that others may review it and hopefully provide feedback to improve it. We sincerely hope that feedback leads to eventual improvements in our low energy data. If you can contribute to this effort and improve EPDL97, or any of our data bases, we would be very interested in collaborating with you.
Format
All of the EPDL97 data is in the form of tabulated data with a defined method of interpolation between tabulated values. Cross sections, form factors and scattering functions are log-log interpolable, and average secondary energies are linear-linear interpolable. In the case of photoexcitation data, it is defined by tabulated discrete energy, strength pairs.
EPDL97 is available in the Livermore ENDL format [37] as well as in the ENDF/B-VI format [38]. These two formats are designed to allow the data to be processed for later use in applications. Note, the excitation data is provided as a separate file and identified as EXDL (Evaluation eXcitation Data Library). This data is only available in the ENDL format; the ENDF/B-VI format does not have any provision for this data.
The data are also available in the simpler EPICSHOW format [6], which is designed to allow the data to be viewed on virtually any computer. Note, earlier versions of the documentation for EPDL were very large and included plots of all of the data. It is no longer economically practical to produce books in this form. However, EPICSHOW has proven to be a very practical replacement for the earlier books of plots of EPDL data.
The original data evaluation was performed in the ENDL format, and EPDL97 in this format includes all of the data discussed above.
After completion of the data evaluation the results were translated from the ENDL to ENDF/B-VI format. The ENDF/B-VI format does not include provisions for average secondary energies. It also does not include provisions of photoexcitation data. Therefore in the ENDF/B-VI format only cross sections, form factors, scattering functions, and anomalous scattering factors are included. The earlier version of EPDL89 in the ENDF/B-VI format only extended up to 100 MeV. Based on many requests from data users, the current version of EPDL97 in the ENDF/B-VI format extends up to 100 GeV.
ENDF/B-VI Photon Interaction Library
The Livermore EPDL data is also the ENDF/B-VI photon interaction library, and EPDL97 is the latest update to this library.
Besides the improvements in the EPDL97 data, one significant difference between the older ENDF/B-VI library and the latest library, is that all of the data in the latest library is in exactly the same form as in EPDL97.
Prior to ENDF/B-VI the ENDF/B photon interaction library represented cross sections as Log X vs. Log Y interpolable between tabulated values. For the first two versions of the ENDF/B-VI photon interaction library, in order to define the total cross section at ALL energies, all cross sections were linearized and the total was defined as the sum of its parts. This turned out to be a poor approach, that introduced significant differences between the original data in the ENDL format and the ENDF/B-VI formatted data.
Starting with this version of EPDL97, the ENDF/B-VI formatted data will use the older ENDF/B convention to represent cross sections in Log X vs. Log Y form, and the total will be defined as the sum of parts ONLY at ALL energies that appear in ANY tabulated partial cross sections.
There are two important results of this procedure,
1) The cross sections in the ENDF/B-VI format are exactly the same as in the ENDL format. The only differences are that in EPDL97 energies are in units of MeV and in ENDF/B-VI in units if eV. The cross sections in both are in barns per atom.
2) The total cross section in the ENDF/B-VI format is equal to the sum its parts ONLY at the tabulated energies, which is the same convention used in earlier versions of ENDF/B. WARNING - do not attempt to define the total cross section between tabulated energies by interpolation. The only correct way to define the total at any given energy is to interpolate each partial cross section and define the total to be the sum of its parts.
Data Units
All cross sections are in units of barns per atom. All energies are in MeV in the ENDL and EPICSHOW formats and eV in the ENDF/B-VI format. Form factors and scattering functions are dimensionless, versus Angstroms. Anomalous scattering factors are dimensionless, versus energy.
Availability
For a copy of this library users at Livermore should contact D. E. Cullen. Users outside of Livermore should contact their local code center, e.g., within the U.S.A., the Radiation Shielding Information Center (RSIC), Oak Ridge National Laboratory.
References
EPDL
[1] D.E. Cullen, S.T. Perkins, and J.A. Rathkopf, "The 1989 Livermore Evaluated Photon Data Library (EPDL)," UCRL-ID-103424, Lawrence Livermore National Laboratory (1990).
[2] D.E. Cullen, et al "Tables and Graphs of Photon-Interaction Cross Sections from 10 eV to 100 GeV Derived from the LLNL Evaluated Photon Data Library (EPDL)," UCRL-50400, Vol. 6, Rev. 4, Part A: Z = 1 to 50 and Part B: Z = 51 to 100, Lawrence Livermore National Laboratory (1989).
[3] D.E. Cullen, S.T. Perkins and E.F. Plechaty, "The ENDF/B-VI Photon Interaction Library," Lawrence Livermore National Laboratory, UCRL-JC-109764, January 1992.
[4] D.E. Cullen, "Photon Interaction Data for ENDF/B-VI," UCRL-JC-116332 and the proceedings of the 1994 Reactor Physics Topical Meeting of the ANS, Feb. 1994.
[5] D.E. Cullen, S.T. Perkins and S.M. Seltzer, "Tables and Graphs of Electron Interaction Cross 10 eV to 100 GeV Derived from the LLNL Evaluated Electron Data Library (EEDL), Z = 1 - 100," Lawrence Livermore National Laboratory, UCRL-50400, Vol. 31, November 1991.
[6] D.E. Cullen, "Program EPICSHOW: A Computer Code to Allow Interactive viewing of the EPIC Data Libraries (Version 94-1)", UCRL-ID-116819, Feb. 1994. EPICSHOW is current available through Data Centers as part of the TART96 CD package. However, current it contains the EPDL89 data. In the coming months it will be updated to contain EPDL97.
[7] J.E. Fernandez, et al., "Polarization Effects on Multiple Scattering Gamma Transport," Radiat. Phys. Chem. 41, 579-630 (1993).
[8] S. Manninen, "Resonant Raman Scattering and Fluorescence Spectroscopy," Radiat. Phys. Chem. 50, 77-89 (1997).
[9] P.M. Bergstrom and R.H. Pratt, "An Overview of the Theories Used in Compton Scattering Calculations," Radiat. Phys. Chem. 50, 3-29 (1997).
[10] B.L. Henke, E.M. Gullikson, and J.C. Davis, "X-Ray Interactions: Photoabsorption, Scattering, Transmission, and Reflection at E = 50 - 30,000 eV, Z = 1 - 92," At. Data Nucl. Data Tables 54, 181-342 (1993).
[11] L. Kissel and R.H. Pratt, "Rayleigh Scattering: Elastic Photon Scattering by Bound Electrons," in Atomic Inner-Shell Physics, B. Crasemann, ed. (Plenum Press, New York, 1985), pp. 465-532.
[12] L Kissel, et al., "The Validity of Form-Factor, Modified Form-Factor and Anomalous-Scattering-Factor Approximations in Elastic Scattering Calculations," Acta Cryst. A51, pp 271-288 (1995).
[13] T. Suric, et al., "Compton Scattering of Photons by Inner-Shell Electrons," Phys. Rev. Lett. 67, pp 189-192 (1991)
[14] P.M. Bergstrom, Jr., et al., "Compton Scattering from Bound Electrons: Full Relativistic Independent Particle Approximation Calculations," Phys. Rev. A 48, pp 1134-1162 (1993).
[15] D.E. Cullen, et al., "Tables and Graphs of Atomic Subshell and Relaxation Data Derived from the LLNL Evaluated Atomic Data Library (EADL), Z = 1 - 100," Lawrence Livermore National Laboratory, UCRL-50400, Vol. 30, October 1991.
[16] D.E. Cullen "Program RELAX: A Code Designed to Calculate X-Ray and Electron Emission Spectra as Singly Charged Atoms Relax Back to Neutrality," Lawrence Livermore National Laboratory, UCRL-ID-110438, March 1992.
[17] J.H. Scofield, "Radiative Transitions," in Atomic Inner-Shell Processes, B. Crasemann, ed. (Academic Press, New York, 1975), pp. 265-292.
[18] E.B. Saloman, J.H. Hubbell and J.H. Scofield, "X-Ray Attenuation cross sections for Energies 100 eV to 100 keV and Elements Z = 1 to Z = 92." At. Data Nucl. Data Tables 38, pp 1-197 (1988).
[19] J.H. Hubbell and S.M. Seltzer, "Tables of X-RAY Mass Attenuation Coefficients and Mass Energy-Absorption Coefficients 1 keV to 20 MeV for Elements Z = 1 to 92 and 48 Additional Substances of Dosimetric Interest," NISTIR 5632, National Institute of Standards and Technology, (1995).
[20] J.H. Hubbell and W.J. Veigele, "Comparison of Theoretical and Experimental Photoeffect Data 0.1 keV to 1.5 MeV," National Bureau of Standards Tech. Note 901 (1976)
[21] J.H. Hubbell, H.A. Gimm, and I. Overbo, "Pair, Triplet, and Total Cross Sections (and Mass Attenuation Coefficients) for 1 MeV-100 GeV Photons in Elements Z = 1 to 100," J. Phys. Ref. Data, Vol. 9, No. 4, pp 1023-1147 (1980).
[22] J.H. Hubbell, et al., "Atomic Form Factors, Incoherent Scattering Functions, and Photon Scattering Cross Sections," J. Phys. Chem. Ref. Data, Vol. 4, No. 3, pp 471-616 (1975).
[23] J.H. Hubbell, et al., "Atomic Form Factors, Incoherent Scattering Functions, and Photon Scattering Cross Sections," J. Phys. Chem. Ref. Data 7, 615 (1977). See also, J.H. Hubbell and I. Overbo, "Relativistic Atom Form Factors and Photon Coherent Scattering Cross Sections," J. Phys. Chem. Ref. Data, 8, 69 (1979).
[24] J.H. Hubbell, "Summary of Existing Information on the Incoherent Scattering of Photons Particularly on the Validity of the Use of the Incoherent Scattering Function," Radiat. Phys. Chem. Vol. 50, No. 1, pp 113-124 (1997).
[25] D.E. Cullen, "Program SCATMAN: A Code Designed to Calculate Photon Coherent Scattering Anomalous Scattering Factors and Cross Sections," Lawrence Livermore National Laboratory, UCRL-ID-103422, November 1989
[26] R.H. Pratt, L. Kissel and P.M. Bergstrom, Jr., "New relativistic S-Matrix results for scattering - beyond the usual anomalous factors/ beyond impulse approximation," in Resonant Anomalous X-Ray Scattering, G. Materlik, C.J. Sparks and K. Fischer, eds. (Elsevier Science Publishers, Amsterdam, 1994), pp 9-33.
[27] A. Costescu, et al., " Retardation and Multipole Effects in Rayleigh Scattering by Hydrogen-like Ions at Low and X-Ray Photon Energies," Phys. Rev. A 50, 1390-1398 (1994).
[28] L. Kissel and R.H. Pratt, "Corrections to Tabulated Anomalous Scattering Factors," Acta Cryst. A46, pp 170-175 (1990).
[29] D.E. Cullen, A.L. Edwards and E.F. Plechaty, "TART95: A Coupled Neutron-Photon Monte Carlo Transport Code," Lawrence Livermore National Laboratory, UCRL-MA-121319, July 1995.
[30] D.E. Cullen, "TART96: A Coupled Neutron-Photon 3-D, Combinatorial Geometry Monte Carlo Transport Code," Lawrence Livermore National Laboratory, UCRL-ID-126455, November, 1996.
[31] J.H. Hubbell, et al., "A Review, Bibliography, and Tabulation of K, L and Higher Atomic Shell X-Ray Fluorescence Yields," J. Phys. Chem. Ref. Data, Vol. 23, No. 2, pp 339-363 (1994).
[32] M.H. Chen, B. Crasemann and H. Mark, "Radiationless Transitions to Atomic M 1,2,3 Shells: Results of Relativistic Theory," Phys. Rev. A, 27, 2989 (1983).
[33] D.E. Cullen, S.T. Perkins and S.M. Seltzer, "Photon and Electron Data Bases and Their Use in Radiation Transport Calculations," Applied Radiation and Isotopes, Vol. 44, No. 10/11, pp. 1343-1347, 1993, Pergamon Press.
[34] D.E. Cullen, "Photon and Electron Interaction Databases and Their Use in Medical Applications," UCRL-JC-117419-D, May 1994, and the proceedings of the 1994 World Conference on Medical Physics and Biomedical Engineering, Rio de Janeiro, Brazil, Aug. 1994.
[35] A. Bielajew and D.E. Cullen, "Incorporating the Livermore Photon Interaction Data Base into the Electron-Photon Monte Carlo Transport Code EGS4," proceedings of the International Conference on Mathematics and Computations, Reactor Physics, and Environmental Analyses, Portland, Oregon, May 1995
[36] D.E. Cullen, "A Simple Model of Photon Transport," Nuclear Instrumentation and Methods in Physics Research B 101 (1995) pp. 499-510
[37] S.T. Perkins and D.E. Cullen, "ENDL Type Formats for the LLNL Evaluated Atomic Data Library, EADL, for the Evaluated Electron Data Library, EEDL, and for the Evaluated Photon Data Library, EPDL," Lawrence Livermore National Laboratory, UCRL-ID-117796, July 1994.
[38] V. McLane, C.L. Dunford and P.F. Rose, "ENDF-102 Data Formats and Procedures for the Evaluated Nuclear Data File, ENDF-6," BNL-NCS-44945, Rev. 11/95, National Nuclear Data Center, Brookhaven National Laboratory (1995).
Appendix
Comparison of EPDL97 and EPDL89
Here we show comparisons between EPDL97 and EPDL89 cross sections for a few elements spread across the periodic table: Z = 10, 30, 60, 90. Comparisons are shown for,
Photoionization
Here you can see that the cross sections are in good agreement, except near edges, and in some cases where more recent calculations and measurements have improved the EPDL97 data; particularly low energy data for outer subshells. The smaller differences (fraction of 1 %) at higher energies are due to more densely tabulated energy points that have improved the EPDL97 data.

Coherent
Here you can see differences, particularly at low energies due to the now available photoexcitation data that was used to calculate the EPDL97 anomalous scattering factors.
Incoherent
Here you can see differences, particularly at low energies due to improved extension of the scattering functions below 100 eV. The smaller differences (fraction of 1 %) at higher energies are due to more densely tabulated energy points that have improved the EPDL97 data.
Pair
Here you can see that the EPDL97 and EPDL89 pair production cross sections are exactly the same.
EPDL97
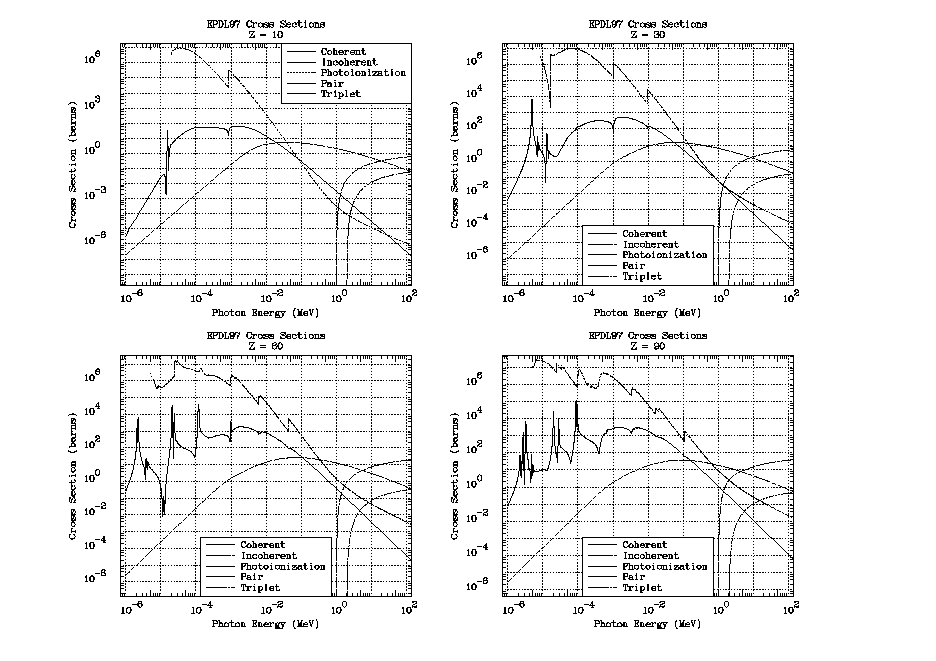
Here you can see the relationship between the cross sections. The variation of the cross sections versus Z is very systematic, so that even from these few examples you will be able to understand the relationship between the cross sections. At low energy photoionization is always the dominant reaction, and coherent is the dominant scattering reaction. In the intermediate energy range incoherent becomes dominant. At high energy pair becomes dominant. Where the dividing line is between low, intermediate and high energy is Z dependent, but from this figure you can get a good idea of what energy range for each process is important versus Z.
Warning - note that below the lowest energy photoionization edge EPDL97 only includes coherent and incoherent scattering defined using the form factor and scattering function approximations. If you want to calculate realistic results NEVER use EPDL97 to perform photon transport calculations in this energy range. You need additional data, that in not included in EPDL97, to perform calculations in this energy range.